[Baekjoon,1219] 오민식의 고민

도시를 방문할 때 마다 이익을 얻거나 손해를 본다. 여기서 출발 도시에서 시작하여 도착 도시로 왔을 때 얻을 수 있는 가장 큰 돈의 액수를 구해야 한다. 이 돈은 사이클을 형성하여 무한대로 얻을 수 있다. 여기서 손해를 최소화 하는 경로를 찾아야 한다고 생각할 수 있다. 즉, 사용하는 비용을 양수로 두고 얻어지는 비용을 음수로 두어 시작점 부터 도착점까지의 최단거리를 찾는 것이다. 이는 음수 간선을 포함하였으므로 최단거리를 찾는 알고리즘 중 벨만-포드의 최단거리 알고리즘을 떠올리게 한다.

사이클이 경로에 없을 수 있다.

이 알고리즘을 그냥 적용하려 하면 문제가 있다. 이 알고리즘은 $V$개의 정점이 있는 그래프에서 $V-1$번 간선들을 완화한 후 한 번 더 완화를 했을 때 완화에 성공하면 음수 사이클이 있다고 판단한다. 하지만 이 문제에서는 음수 사이클이 존재한다고 해서 항상 가중치가 음의 무한대인 경로가 있는 것은 아니다. 예를 들어 아래의 그래프를 형성하는 입력을 보자.

//input
5 0 2 5
0 1 2
1 2 2
3 1 1
3 4 1
4 3 1
0 0 0 1 8
//output : -4

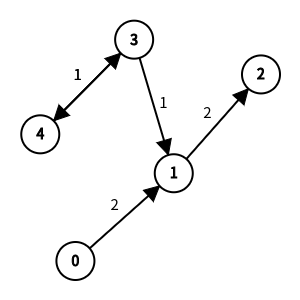
3번 정점과 4번 정점으로 도착하면 취해지는 이득이 각각 1과 8이므로 음수 사이클이 형성된다. 하지만 시작 정점에서 도착 정점으로 가는 경로는 $0-1-2$ 인데, 음수 사이클에 방문할 수 없다. 하지만 이를 고려하지 않는다면 음수 사이클이 있다고 판단할 것이고 잘못된 결과를 출력할 것이다.

이를 해결하는 방법은 $V$번째 완화가 성공 시 완화가 성공한 정점이 시작 지점과 도착 지점을 잇는 경로가 존재하는 지 판단하는 것이다. 경로가 있는 지 판단은 모든 정점의 쌍에 대해 한 정점에서 다른 정점으로 도달 가능 여부를 저장하는 배열 $reachable[][]$을 이용하면 된다. 이 배열은 플로이드의 최단 거리 알고리즘을 적용하여 형성하면 된다.

#include <iostream>
#include <vector>
#include <cstring>
#include <climits>
using namespace std;

const int MAX_V=100;

int V;
vector<pair<int,int> > adj[MAX_V];
bool reachable[MAX_V][MAX_V];
int sales[MAX_V];

long long bellmanFord(const int start, const int target)
{
    vector<long long> upper(V,LONG_MAX);
    // 시작 위치에서 판매를 하고 출발한다. 
    upper[start]=-sales[start];
    for(int iter=0;iter<V;++iter)
        for(int here=0;here<V;++here)
            // 현재 경로가 없는 정점은 완화하지 않는다. 
            if(upper[here]<LONG_MAX)
                for(int i=0;i<adj[here].size();++i)
                {
                    int there=adj[here][i].first;
                    int cost=adj[here][i].second-sales[there];
                    if(upper[there]>cost+upper[here])
                    {
                        // 음수 사이클 존재 여부 판단 
                        if(iter==V-1 && reachable[start][here] && reachable[here][target])
                            return -LONG_MAX;
                        upper[there]=cost+upper[here];
                    }
                }
    return upper[target];
}

int main()
{
    int start, target, m;
    cin>>V>>start>>target>>m;
    
    memset(reachable,false,sizeof(reachable));
    for(int i=0;i<V;++i)
        reachable[i][i]=true;
    
    for(int i=0;i<m;++i)
    {
        int a,b,c;
        cin>>a>>b>>c;
        // 비용의 최소 값을 얻어야 하니 양수로 
        adj[a].push_back(make_pair(b,c));
        reachable[a][b]=true;
    }
    for(int i=0;i<V;++i)
        cin>>sales[i];
    
    // 플로이드 알고리즘을 이용한 경로 존재 여부 배열 형성 
    for(int k=0;k<V;++k)
        for(int i=0;i<V;++i)
            for(int j=0;j<V;++j)
                reachable[i][j]|=reachable[i][k]&&reachable[k][j];
    
    long long ret=bellmanFord(start,target);
    // 음수 사이클인 경우 
    if(ret==-LONG_MAX)
        cout<<"Gee"<<endl;
    // 경로가 존재하지 않는 경우 
    else if(ret==LONG_MAX)
        cout<<"gg"<<endl;
    else
        cout<<(-ret)<<endl;
    
    return 0;
}

---

삽질

현재 경로가 형성되지 않은 정점에 대해서 완화를 시도하면 안된다. 즉, $upper[here]$이 $INF$인 정점 $here$에 대해 완화를 시도하지 않는 것이다. 이를 적용하지 않으면 아래와 같은 일이 발생한다.

• 시작 지점에서 도착 지점으로 가는 경로가 존재하지 않는 데 완화 시 $INF$보다 약간 작은 값이 되어 경로가 있다고 판단한다.

또한 위와 동시에 $V$번째 완화 시 도달 가능 여부를 판단할 때 $there$을 기준으로 하면 아래와 같은 일이 발생한다.

• $INF$를 해당 형의 최대 값으로 설정하였을 때, $upper[here]=INF$ 인 정점 $here$에서 양수 간선으로 이어진 다음 정점이 도착 지점과 현재 지점으로 연결된 경우 $upper[here]+cost$가 범위를 넘어 음수 값으로 잘못 반환되어 완화가 발생할 수 있다. 이는 음수 사이클이 있다고 잘못 판단될 수 있다. 예를 들어 위에서 설명한 그래프의 입력 값을 돌려 보면 $V$번째 완화 시 오버플로가 발생하여 3번 정점에서 1번 정점을 향하는 간선이 완화된다.

---

참고

• 구종만, 프로그래밍 대회에서 배우는 알고리즘 문제해결 전략, 2012, 인사이트